Lista de alumnos/alumnas inscriptos/as en Matemática (previa)- para Julio 2017
Fechas de las pruebas parciales. |
Matemática
de 1° Año PREVIA para JULIO
|
Matemática
de 2° Año PREVIA para JULIO
--------------------------------------------------------------------------
Matemática de 3° Año PREVIA para JULIO
Para rendir cada prueba, deben tener al menos 2 consultas
Primera prueba - LUNES, 24 de abril de 2017.
a las 13horas
Recuperación de la Primera prueba el lunes, 8 de mayo a las 13 horas --------------- Segunda prueba - Lunes 22 de mayo de 2017- Regla de Ruffini- Teorema del resto Productos especiales ( cuadrado y cubo de un binomio - producto de una suma y una diferencia) Ver los videos y resolver el práctico |
Matemática de 4° Año PREVIA para JULIO
Para rendir cada prueba, deben tener al menos 2 consultas
Primera prueba - LUNES, 24 de abril de 2017
a las 13,30 horas
Recuperación de la Primera prueba el lunes,
8 de mayo a las 13,15 horas
---------------
Segunda prueba - Lunes 22 de mayo de 2017-
a las 13,15 horas
Función cuadrática
---------------------------------------------------------------------------------------------------------------
Matemática de 5° Año PREVIA para JULIO
Para rendir cada prueba, deben tener
al menos 2 consultas
Primera prueba - Martes, 25 de abril de 2017
a las 13,20 horas
Recuperación de la Primera prueba el Martes, 9 de mayo a las 13,20 horas |
Empezamos con MATEMÁTICA PREVIA
para 3°, 4° y 5° Año
para 3°, 4° y 5° Año
Busquemé e inscríbase.
Lo primero es tener ganas de estudiar,
entra en esta blog,ahí encontrarás las indicaciones!!!!!
Busca en el Archivo del blog: 2015 ( 6)
" el hábito del querer (la fortaleza de decir
sí a nuestras cosas más importantes)
y no al querer (la fortaleza de decir no a
cosas menos importantes, y a la presión de los
compañeros)."
Busca en el Archivo del blog: 2015 ( 6)
Te dejo un pensamiento
sí a nuestras cosas más importantes)
y no al querer (la fortaleza de decir no a
cosas menos importantes, y a la presión de los
compañeros)."
Para cada evaluación te debes ayudar
con los apuntes,
consultas y ejercicios que hay en este
consultas y ejercicios que hay en este
blog o en el blog del año correspondiente
y por supuesto
y por supuesto
¡ASISTE A LAS CLASES DE APOYO!
No pierdas tiempo es tu oportunidad!!
Tu PROFE Susana
Lista de alumnos/ alumnas
inscriptos/as en 4° año
para Julio 2017
3° AÑO Prueba N°1
Expresiones algebraicas
Operaciones: suma, resta, multiplicación y división entre polinomios.
1° EXAMEN de la previa de 3er. Año Primera prueba - LUNES, 24 de abril de 2017. a las 13horas....... !
Recuperación de la Primera prueba el lunes, 8 de mayo
a las 13 horas
---------------
Segunda prueba - Lunes 22 de mayo de 2017-
Regla de Ruffini- Teorema del resto
Productos especiales ( cuadrado y cubo de un binomio -
producto de una suma y una diferencia)
Ver los videos y resolver el práctico
Prueba N° 2
Regla de Ruffini. Teorema del resto.
Productos especiales: cuadrado de un binomio. Cubo de un binomio. Producto de una suma por una diferencia.
2° EXAMEN de la previa 3er.Año Lunes ....a las 13hs...!!! Después!!!! cuando aprobemos!!!!
Prueba N° 3
Teorema de Pitágoras. Problemas de aplicación.
Notación científica. Redondeo y truncamiento.
3° Examen de la previa Lunes ....a las 13hs...!!! TENGO APUNTES, SI NECESITAS FOTOCOPIAS. TIENES QUE HABLAR CON TU PROF. SUSANA
Prueba N°4
Proporcionalidad :
Regla de tres simple: directa e inversa.
Problemas. Ecuaciones
Función lineal: pendiente, ordenada al orígen.
Gráfico con tablas en un par de ejes cartesiano
TRABAJO PRÁCTICO PARA LA PRUEBA N°4 (presentación antes del día - con la defensa de un ejercicio ante la profesora Susana, por sorteo) Lee, razona, escribe y clasifica la proporción(directa e inversa). Resuelve. 1) En una panadería, con 80 kilos de harina hacen 120 kilos de pan. ¿Cuántos kilos de harina serían necesarios para hacer 99 kilos de pan? 2) En un plano de una ciudad, una calle de 350 metros de longitud mide 2,8 cm. ¿Cuánto medirá sobre ese mismo plano otra calle de 200 metros? 3) En el equipo de fútbol del barrio han jugado como arqueros Ángel y Diego. A Ángel le han marcado 13 goles en 10 partidos jugados. Diego jugó 15 partidos y le marcaron 18 goles. ¿Cuál de los dos ha tenido mejores actuaciones? 4) Una piscina portátil ha tardado en llenarse seis horas utilizando cuatro grifos iguales. ¿Cuántos grifos, iguales a los anteriores, serían necesarios para llenarla en 3 horas? 5) Para construir una casa en ocho meses han sido necesarios seis albañiles. ¿Cuántos habrían sido necesarios para construir la casa en tan sólo tres meses? 6) En una fábrica automovilística, una máquina pone, en total, 15.000 tornillos en las 8 horas de jornada laboral, funcionando de forma ininterrumpida. ¿Cuántos tornillos pondrá en 3 horas? Para resolver este ejercicios mira en el blog "Teorema de Thales" 7) Sabiendo que las rectas r, s y t son paralelas, la longitud de x es: 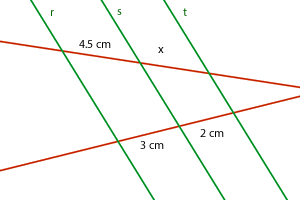 |
Lista de alumnos/ alumnas
inscriptos/as en 3° año
para Julio 2017
Nombre
|
Apellido
|
D.N.I.
|
Curso actual
|
Curso
rinde
|
1°
Prueba
|
2°
Prueba
|
3°
Prueba
|
4°
Prueba
|
Nota
Final
|
1.Selena | Flores | 43.953.510 | 4°A | 3°año | No se presentó | ||||
2.Nuria | Garro | 43.620.835 | 4°A | 3°año | No se presentó | ||||
3.Magalí | Aguilar | 43.157.925 | 4°A | 3°año | Recupera | ||||
4.Yohana | Sosa | 43.123.597 | 4°A | 3°año | Aprobó 8(ocho ) | ||||
5.Florencia | Astullido | 42.999.997 | 4°A | 3°año |
No se presentó
| ||||
6.Tomás | Garro | 42.799.662 | 5°E | 3°añoB |
No se presentó
| ||||
7.Facundo | Vallejos | 43221922 | 5°E | 3°año |
No se presentó
| ||||
8.Alexis | Lucero | 43359899 | 4°E | 3°año |
No se presentó
| ||||
9.Cynthia | Zanglá | 42.976.683 | 4°B | 3°año |
No se presentó
| ||||
41.841.643 | 4°E | 3°año | |||||||
43.123.565 | 4°E | 3°año | |||||||
Lista de alumnos/ alumnas
inscriptos/as en 3° año
para Julio 2017
inscriptos/as en 3° año
para Julio 2017
Nombre
|
Apellido
|
D.N.I.
|
Curso actual
|
Curso
rinde
|
1°
Prueba
|
2°
Prueba
|
3°
Prueba
|
4°
Prueba
|
Nota
Final
|
Lucas | Mendoza | 44.019.788 | 4°B | 3°añoB | No se presentó | ||||
Ana Paula | López | 43.490.497 | 4°B | 3°añoA | No se presentó | ||||
Brenda | Pereira | 42.909.978 | 4°B | 3°añoB |
No se presentó
| ||||
Matías | Tobares | 42.620.577 | 4°B | 3°añoD | No se presentó | ||||
Eber | Perez | 42.562.442 | 4°B | 3°añoD |
No se presentó
| ||||
Melany | Jofré | 43.551.640 | 4°B | 2°añoA |
No se presentó
| ||||
Candela | Garay | 42.976.768 | 4°B | 2°añoA |
No se presentó
| ||||
xxxxx | 3°año | ||||||||
Lista de alumnos/ alumnas
inscriptos/as en 3° año
para Julio 2017
Nombre
|
Apellido
|
D.N.I.
|
Curso actual
|
Curso
rinde
|
1°
Prueba
|
2°
Prueba
|
3°
Prueba
|
4°
Prueba
|
Nota
Final
|
Alexander | Villa | 43.840.232 | 4°E | 3°añoB | No se presentó | ||||
Gabriel | Lopez | 43.072.968 | 4°E | 3°añoB | No se presentó | ||||
Facundo | Ferreyra | 43.831.418 | 4°E | 3°añoD y 2°añoD | No se presentó | ||||
Jorge | Díaz | 43.840.192 | 4°E | 3°añoD | No se presentó | ||||
Rosario | Mercau | 43.753.697 | 4°E | 3°añoB |
No se presentó
| ||||
María | Calderón | 43.690.9o3 | 4°E | 3°añoA |
No se presentó
| ||||
Alexis | Orozco | 43.359.830 | 4°E | 3°añoB | No se presentó | ||||
xxxx | 3°año | ||||||||
xxxxx | 3°año | ||||||||
3°año |
Matemática PREVIA de: "Cuarto AÑO"
Primera prueba: función lineal
Debes saber:
Primera prueba - LUNES, 24 de abril de 2017.
a las 13,30 horas....... !
Recuperación de la Primera prueba el lunes,
8 de mayo a las 13,15 horas
---------------
Segunda prueba - Lunes 22 de mayo de 2017-
a las 13,15 horas
Función cuadrática
------------------ 1) Ubicar puntos en un sistema de ejes cartesianos. 2) Reconocer una función lineal y cuadrática. 3) Trabajar con tablas . 4) Graficar funciones lineales y cuadrática. 5) Definir y encontrar ecuaciones de rectas que pasan por un punto y por dos puntos. 6) Encontrar y graficar rectas paralelas y perpendiculares a un recta. 7) Indicar intervalos de crecimiento y decrecimiento, de positividad y negatividad, máximos y mínimos. 8)Reconocer los coeficientes de los términos a, b y c, Vértice de la parábola, eje de simetría, la ordenada al orígen , las raíces de la función.
Prático N°1
FUNCION CUADRATICA
CORRIMIENTOS Y FORMA CANONICA
En los siguientes ítems se propone comparar una función cuadrática con la más sencillas de todas ellas, que es y=x2.
Ya vimos que cuando la variable cuadrática está acompañada por un números (coeficiente), es decir, y = a.x2 si ese número es mayor que cero, es decir, es positivo, las ramas de la curva abren hacia arriba. Por el contrario si ese número es menor que cero, es decir, es negativo, las ramas abren hacia abajo. En todos los casos el vértice de la gráfica es el punto (0,0).
Ahora observemos el grafico dela función cuadrática de la forma y = ( x-2)2.La curva se “corre” dos lugares hacia la derecha.
Si fuera y = (x+2)2, ¿hacia dónde y cuántos lugares se “correría?. Dibújala para verificar. ¿Cuál es el vértice en ambas graficas? Dar sus coordenadas.
Por lo tanto responde:
1- ¿A cuál de las formulas podría corresponder el siguiente grafico? Justifica tu elección.
y = ( x – 10)2
En una función cuadrática y = ax2 + bx + c el vértice es el punto V=(p,q), entonces la función puede escribirse como y = a ( x-p )2 + q. ESTA FORMA DE ESCRIBIR LA CUADRATICA SE LLAMA FORMA CANONICA DE LA FUNCION.
2- Entonces, ¿Cómo sería el vértice de la parábola y = ( x – 2 )2 + 1? ¿Y si fuese
y = (x – 2 )2 +2? ¿Y si fuera y = (x-2)2 + 3?
Para lograr una tabla de valores que sean realmente efectivos para lograr el grafico dela función cuadrática en forma canónica, se deben tomar valores alrededor de la coordenada x del vértice. Es decir se podría tomar dos valores a la izquierda de la coordenada x y dos valores a la derecha de la coordenada x, incluida x.
3- Ahora realiza el gráfico dela siguiente parábola: y = (x-2)2 +1. También grafica
y = (x – 2 )2+2 ; y = (x-2)2 + 3.
4- ¿Cuáles son las coordenadas del vértice de la parábola que queda determinada al graficar la función y = (x-4)2 + 6? ¿Y si fuese y = (x + 4)2 +6?
5-
Y = ( x + 9 )2 + 8
Y = ( x - 9 )2 + 8
Y = ( x - 8 )2 + 9
Y = ( x + 8 )2 +9
Y = ( x - 8 )2 -9
Y = ( x - 9 )2 – 8
6- Decidí cuál de los gráficos corresponde a cada ecuación cuadrática.
a) y = x2 + 1 b) y= - x2 + 1 c) y = x2 – 1
7- El siguiente grafico corresponde a la función y = (x – 1)2.
y = -2 . (x – 1)2.
Analiza diferencias y semejanzas.
b) ¿Sera cierto que el grafico de la función y = 2. (x – 1)2 + 8 es igual al de y = 2 . (x – 1)2 pero desplazado 8 unidades hacia arriba? ¿Cómo te das cuenta?
c) ¿Cuál de los gráficos que se muestran podría corresponder a la función
y = - 2. (x – 1)2 + 8? ¿Cómo pueden darse cuenta sin graficar?
FUNCION CUADRATICA COMPLETA
Representación de la función cuadrática dada por la fórmula completa y = a.x 2 + bx + c donde a, b y c son números reales. Para realizar el grafico de esta función utilizaremos un método basado en determinar puntos notables de la gráfica de y.
· Vértice de la parábola. Lo identificaremos con coordenadas xv e yv, es decir
V = (xv , yv)
xv =
· Raíces de la parábola. Son los puntos de intersección de la parábola con el eje x. Vale decir y = 0. Es decir se debe igualar a 0 la función, a saber a.x 2 + bx + c = 0.
Eso equivale a resolver dicha ecuación utilizando la formula resolvente para una ecuación de segundo grado completa. Recordemos dicha fórmula:
X1,2 =
· Eje de simetría: es la recta que tiene por ecuación: x = xv
· Ordenada al origen: es el punto de intersección (corte) de la gráfica con el eje y, vale decir que es y(0) = c
·
Vértice: xv =
Raíces:
Eje de simetría: x = -1
Ordenada al orígen: 02 + 2 . 0 – 3 = -3
Ahora la grafica:
Raíces de la función cuadrática
Cuando se grafica una función cuadrática, puede ocurrir que la parábola tenga contacto con el eje x en dos puntos, en un solo punto o bien no tenga contacto. Se les llama raíces de la función o ceros de la función.
Para ello se analiza la expresión b2 – 4.a.c que se denomina discriminante. Puede pasar:
b2 – 4.a.c > 0, la función tiene dos raíces reales ( la gráfica corta al eje x en dos puntos)
b2 – 4.a.c = 0, la función tiene una única raíz real ( la gráfica corta en un sólo punto)
b2 – 4.a.c < 0, la función no tiene solución real ( la gráfica no corta al eje x)
8- Grafiquen las siguientes funciones cuadráticas, luego comprueba tu producción con el
GEOGEBRA, guardar como (Func.Cuad. N.A.Curso División ) y enviar para su corrección:
a) y = x2 – 5x + 6 b) y = - x2 + 4x
c) y = x2 – x + ¼ d) y = x2 + x + 1
9- Sin resolverlas, indiquen el tipo de raíces de cada una de estas ecuaciones:
a) x2 – x + 2 = 0 b) y = x + 9x2 – 1 = 0 c) y = - 2 x2 – 6x
Forma factorizada de una función cuadrática
Se llama forma factorizada de una función cuadrática a la expresión:
y = a . (x –x1) . (x – x2)
Donde a es el coeficiente principal, es decir, el número que acompaña a x2 y x1 y x2 son sus raíces.
10- En cada caso halla la forma factorizada de la función cuadrática que cumple las
condiciones indicadas:
a) El coeficiente principal es 2, y sus raíces son 0 y -4
b) El coeficiente principal es 2/3 y su única raíz es 5.
c) Utiliza el programa GEOGEBRA para graficarlas. Guárdalas en una carpeta y envíalas para su corrección.
11- Decidí a cuales de los gráficos corresponde cada formula:
a) Y = - (x – 1)(x + 1) b) y = (x – 1)( x + 1)
c) y = – (x – 1)2 d) y = (x + 1)2
-------------------------------------------------------
Prueba integradora
Función cuadrática
Me pides todas las ecuaciones cuadráticas!!!
Actividad N°1
Resuelvan las
siguientes ecuaciones e indica cuantas raíces pueden tener :
Actividad N°2
En las siguientes
funciones cuadráticas:
a) Dar las
coordenadas del vértice
b) Escribe la forma canónica y grafica por desplazamientos horizontales y verticales la función. Actividad N°3
En las siguientes
funciones cuadráticas:
a) Encuentra las
coordenadas de los puntos de corte de la parábola con los ejes cartesianos.
b) Escribe en forma
factorizada la función y realiza el gráfico en un par de ejes cartesianos.
Actividad N°4
Escriba las
siguientes funciones en la forma más conveniente de acuerdo con los datos dados
y luego hallen las expresiones polinómicas de cada una. Grafica en
un par de ejes cartesianos para prácticar.
a) El vértice es V= ( -3, -2) y el coeficiente principal es -2 b) Las raíces son X1 = - 4 y X2 = 2 y el coeficiente principal es -1. c) El vértice es ( -5, 4) y el coeficiente principal es -3. d)El vértice es (3, -2) y el coeficiente principal es 1/2 Actividad N°5
Expresen cada una de
las siguientes funciones en la forma en que se pide.
a) y = - x2 + 2x + 3, en forma canónica es y = .............. b) y = x2 -4x + 4, en forma factorizada es y = ................
------------------------------------------------
Prático N°2
Trabajo práctico (para repasar ) FUNCIÓN LINEAL
Actividad N°1
Para cada una de las rectas, determinar la pendiente y ordenada al orígen. Grafica en un par de ejes cartesianos con diferentes colores.
a) x - 5y = 20 b) y = -1 c) 3y + x - 6 = 0
d) y = (1/2) x + 2 e) y + 2 = 4x f) (3/2)x + y = 5
Actividad N°2
Escribe la ecuación de la recta que pasa por un punto y tiene pendiente m.
a) T=( 5,-2) m=4 b) S=(1,2) m=-2
c) P=(2,1/2) m=-3 d) A=(2,0) m=-1/3
Actividad N°3
Escribe la ecuación de la recta que pasa por dos puntos dados y luego grafica la recta y el comprueba que el punto pertenece a ella.
a) P=(-2,-3) y Q=(-4,1) b) S=(-5,2) y T=(2,3)
c) R=(3,-2) y B=(2,-6) d) C=(0,0) y D=(1,-1)
Actividad N°4
¿Cuál de las siguientes ecuaciones corresponde a la de una recta perpendicular a la R: 3x - 2y = 0 que pasa por el punto P=(-3,5)?
a) -3x + 2y = 19 b) 2x + 3y = 9
c) 3x - y = -4 d) 2x + 3y = 21
Actividad N°5
Hallar la ecuación la ecuación de una recta paralela y otra perpendicular a la dada que pase por los puntos indicados. Graficar a) y c)
a) y = 4x - 2 P=(2,1) b) 2x + y = 3 Q=(1,-2)
c) y =(-3/2)x +1 R=(1/2,3) d) 5/2x - y = 4 S=(5,-1)
Ejercitación: Modelo de evaluación
Hallar la ecuación de : a) Una recta A que pasa por los puntos H=(-3. 2) y P=( -5, 3) b) Una recta B // A que corta al eje x en x= 3 c) Grafica en un par de ejes cartesianos las rectas A y B, los puntos H y, P y el punto de corte con el eje x. Actividad N°2 Encuentra dos rectas C y D, que son perpendiculares. La recta C tiene pendiente -2 y pasa por el punto T=( -2, 1) y la recta D pasa por el punto F=( 3, -2). Grafica en un par de ejes cartesianos las rectas C , D y los puntos T y F. Actividad N°3 Dada la recta R: 2y + 5x - 4 =3, encontrar la ecuación de una recta A // R y pasa por el punto T =( -1, 1). Graficar la situación planteada. |
inscriptos/as en 4° año
para Julio 2017
Nombre | Apellido | D.N.I. | Cursa en: | Previa de: |
Prueb. N°1
Función lineal |
Prueb. N°2
Sistema de dos ecuac. con dos incógnitas |
Prueb.N°3
Función cuadrática.Ecuac. e inec. con módulo |
Resultado final
|
Camila
|
Gitto
|
43.490.265
|
5°A
|
cuarto
| Recupera | |||
Lucrecia
|
Miranda
|
42.799.977
|
5°A
|
cuarto
|
Aprobó
8(ocho) | |||
Yamila
|
Bognar
|
43.072.512
|
5°A
|
cuarto
|
No se presentó
| |||
Celina
|
Gallardo
|
42.991.053
|
5°A
|
cuarto de otra escuela
|
Recupera
| |||
Candela
| Pereira |
42.632.449
|
5°A
|
cuarto
| Recupera | |||
Brisa
|
Ballejos
|
42.562.433
|
5°A
|
cuarto
|
No se presentó
| |||
Oriana
|
Avila
|
43.254.110
|
5°A
|
cuarto
|
No se presentó
| |||
Ignacio
|
Morales
|
42.142.204
|
5°A
|
cuarto
| No se presentó | |||
Lautaro
|
Albornoz
|
43.343.129
|
5°A
|
cuarto
|
Aprobó
9(nueve) | |||
Dahyana | Barrera | 42.976.605 | 5°A | cuarto |
Aprobó
8(ocho) | |||
Marianela | Godoy | 43.552.120 | 5°A | cuarto | Aprobó 7(siete) | |||
xxxx | 5°A | |||||||
Lista de alumnos/ alumnas
inscriptos/as en 4° año
para Julio 2017
Nombre | Apellido | D.N.I. | Cursa en: | Previa de: |
Prueb. N°1
Función lineal |
Prueb. N°2
Sistema de dos ecuac. con dos incógnitas |
Prueb.N°3
Función cuadrática.Ecuac. e inec. con módulo |
Resultado final
|
Cynthia
|
Zanglá
|
42.976.683
|
5°B
|
cuarto
| No se presentó | |||
Cyntia
|
Pereyra
|
43.551.866
|
5°B
|
cuarto
|
Recupera
| |||
Melina
|
Miguez
|
43.490.161
|
5°B
|
cuarto
|
Recupera
| |||
Marcelo | Ortubia | 42.909.177 |
5°B
|
cuarto
|
Recupera
| |||
Lautaro
| Tapia |
43.881.821
|
5°B
|
cuarto
|
Recupera
| |||
Luca
|
Sosa
|
43.123.743
|
5°B
|
cuarto
|
Recupera
| |||
Facundo
|
Fernandez
|
43.359.719
|
5°B
|
cuarto
| Recupera | |||
Ignacio
|
Fernandez
|
42.142.204
|
5°B
|
cuarto
|
No se presentó
| |||
Lautaro
|
Albornoz
|
43.343.129
|
5° A
|
cuarto
|
5°A
| xxxxx | xxxx | |
Noemí
|
Campos
| 41.443.273 | 5°B | cuarto | No se presentó | |||
Gilda | Sanchez | 41.920.361 | 5°B | cuarto | Aprobó 7(siete) |
Lista de alumnos/ alumnas
inscriptos/as en 4° año
para Julio 2017
Nombre | Apellido | D.N.I. | Cursa en: | Previa de: |
Prueb. N°1
Función lineal |
Prueb. N°2
Sistema de dos ecuac. con dos incógnitas |
Prueb.N°3
Función cuadrática.Ecuac. e inec. con módulo |
Resultado final
|
Rodrigo
|
Fernandez
|
41.919.558
|
5°E
|
cuarto E
| No se presentó | |||
Facundo
|
Vallejo
|
42.991.377
|
5°E
|
TERCERO ? y cuarto E
|
1ero. inscripto 3°año
| |||
Estefani
| Escudero |
43.072.505
|
5°E
|
cuarto E
|
No se presentó
| |||
Tomás
|
Garro
|
42.799.662
|
5°E
|
TERCERO
|
Inscripto
3° año | |||
Karen
| Rosales |
41.341.643
|
5°E
|
cuarto E
|
No se presentó
| |||
Jenifer
|
Rosales
|
43.123.565
|
5°E
|
cuarto E
|
No se presentó
| |||
Abigail
| Villegas |
42.991.088
|
5°E
|
cuarto E
|
Recupera
| |||
FlorenciaG.
| Villegas |
43.221.922
|
5°E
|
cuarto E
|
Recupera
| |||
Leonel
| Puebla |
42.168.410
|
5°E
|
cuarto E
| No se presentó | |||
Agustín
| Zabala | 43.123.688 | 5°E | cuarto E | Recupera |
Matemática PREVIA de: "Quinto AÑO"
Lista de alumnos/ alumnas
inscriptos/as en 5° año
para Julio 2017
Nombre | Apellido | D.N.I. | Cursa en: | Previa de: |
Prueb. N°1
Función lineal |
Prueb. N°2
Sistema de dos ecuac. con dos incógnitas |
Prueb.N°3
Función cuadrática.Ecuac. e inec. con módulo |
Resultado final
|
Natasha
|
Sosa
|
41.807.453
|
6°A
|
quintoA
| ||||
Analia
| Urquiza | 41.272.813 | 6°A | quintoA | ||||
Camila | Torres |
41.504.275
|
6°A
|
quintoA
| ||||
Nicolás
|
Pereyra
|
42.486.644
|
6°A
|
quintoA
| ||||
xxxxx
|
6°A
| quintoA | ||||||
6°A | quintoA | |||||||
xx
|
6°A
|
quintoA
| ||||||
xxxxxx
|



